Did you solve it? Naughty knights | Mathematics

Earlier today I present you these problems from the Mathigon puzzle advent calendar. Here they are again with solutions.

1. The knights move in.

Solution

2. Round the missing numbers.

Solution

Each number is the sum of the previous two numbers. 1 + 3 = 4, 3 + 4 = 7, and so on. It is just like the Fibonacci series, which obeys the same rule, but starts 0, 1.

3. Are you square?

Solution

4. Hexagonal, hexagonal, hexagonal.

Solution 3/16

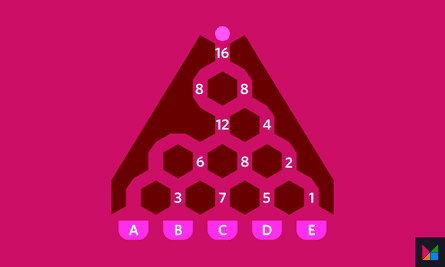
5. Satsuma segment

Solution 25/16

This one requires a little more work. You will also need to use Pythagoras’ theorem for right triangles: the square of the hypotenuse is equal to the sum of the squares on the other two sides. The first thing is to expand the half circle to show the full circle, and draw in the triangle below. The circle meets the left side of the square in the middle. The left angle of the triangle is a right angle because every point on a circle subtends a right angle with the diameter.

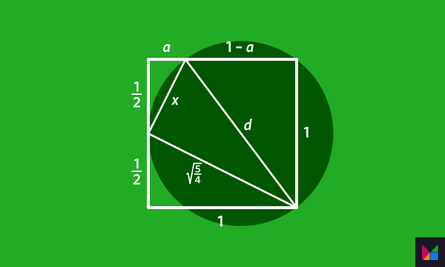
So d² = a² + (1/2)² + 5/4

and d² = (1 – a)² + 1

So a² + 6/4 = 1 – 2a + a² + 1

2a = 2 – 6/4 = 1/2

a = 1/4, and when you plug in this value d² = 25/16, so d = 5/4

I hope you enjoyed today’s puzzles. I’ll be back in two weeks… on Christmas Day!

Thanks to Mathigonwhich belongs to international edtech firm Strengthen. Mathigon is one of the most engaging and creative math resources on the web, and it’s free. Check it out!

I’ve been doing a puzzle here on alternate Mondays since 2015. I’m always on the lookout for great puzzles. If you want to suggest one, email me.